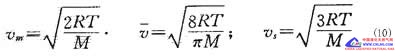随着科学技术的发展、特别是近年来计算机和微电子学、生物工程、材料科学、表面科学、航天和航海工程等高技术科学的发展,对真空科学要求越来越高。真空科学做为这些高技术发展不可缺少的技术必将起到更加重要的作用。例如,在目前微电子学及其纳米级电子材料和元器件的发展中。对真空系统不仅要求采用高真空、超高真空和真空气氛清洁无油,而且要求耐腐蚀、耐粉尘。为了适应这些要求,在真空获得设备中制造各种于式泵、耐腐蚀泵,进一步发展磁悬浮式分子泵和能够避免强磁场及等离子体对涡输分子泵金属转子产生涡流发热的用陶瓷做成转子的新型分子泵,是很必要的。在真空测量方面,我国与国外也存在较大的差距,主要表现在真空规管的结构,电子线路的设计,集成电路和自动换挡及数字显示等新技术的采用上。因此尽快的改变我国真空测量仪器的现状,促进这一技术向多用化、自动化及体积小、外形美等方面发展,也是一个重要的问题。此外,追赶当前国际上在极高真空测量和特殊条件下的真空测量颈域中的先进水平、也是我国真空工作者一项责无旁贷的艰巨任务。
真空物理基础(上) 作者:张世伟
对于任何一种真空产品或一项真空工艺,都有着专门的物理知识作为其工作原理的基础。但本次讲座所要介绍的,仅仅是那些在真空行业的各个领域中都会经常遇到的最基本的物理知识。主要包括气体及蒸汽的性质及其内部各种动力过程的规律(空间过程)、气体与固体间的作用规律(器壁过程)以及气体流动的规律。限于篇幅,每个方面只能作简单的介绍。
一、理想气体定律
首先应该说明,本节及以后几节中所介绍的定律和公式,是针对平衡状态下的理想气体得出的。不过,常温(与室温相比)低压(相对大气压而言)下的各种气体都可以看作是近似程度相当好地理想气体,因此,我们可以放心地把这些定律和公式应用于真空工程的绝大部分计算之中。这其中包括通常所涉及到的各种气体,甚至于接近饱和的蒸汽(如水蒸汽);也包括各类气体状态过程,甚至于明显的非平衡状态(如气体的流动过程)。
气体的压力p(Pa)、体积V(m3)、温度T(K)和质量m(kg)等状态参量间的关系,服从下述气体实验定律:
1、波义耳~马略特定律:一定质量的气体,若其温度维持不变,气体的压力和体积的乘积为常数
pV = 常数 (1)
2、盖·吕萨克定律:一定质量的气体,若其压力维持不变,气体的体积与其绝对温度成正比
V/T = 常数 (2)
3、查理定律:一定质量的气体,若其体积维持不变,气体的压力与其绝对温度成正比。
p/T = 常数 (3)
上述三个公式习惯上称为气体三定律。具体应用方式常为针对由一个恒值过程连结的两个气体状态,已知3个参数而求第4个参数。例如:初始压力和体积为P1、V1,的气体,经等温膨胀后体积变为V2,则由波义耳--马略特定律,可求得膨胀后的气体压力为P2 = P1V1/V2。这正是各种容积式真空泵最基本的抽气原理。
4、道尔顿定律:相互不起化学作用的混合气体的总压力等于各种气体分压力之和。
P = P1+ P2+····+ Pn (4)
这里所说的混合气体中某一组分气体的分压力,是指这种气体单独存在时所能产生的压力。
道尔顿定律表明了个组分气体压力的相互独立和可线性叠加的性质。
5.阿佛加德罗定律:等体积的任何种类气体,在同温度同压力下均有相同的分子数;或者说,在温度同压力下,相同分子数目的不同种类气体占据相同的体积。1mol任何气体的分子数目叫做阿佛加德罗数,NA =6.022×1023mol-1。在标准状态下(po= 1.01325×105Pa,To = 0oC),1mol任何气体的体积称为标准摩尔体积,Vo = 2.24×10-2m3mol-1。
根据上述气体定律,可得到反映气体状态参量p、V、T、m之间定量关系的理想气体状态方程:
pV =m/M(RT) (5)
式中的M为气体的摩尔质量(kg/mol),R为普适气体常数,R=8.31J/(mol·K)。在已知p、V、T、m四参量中的任意三个量时,可由此式求出另外一个值。例如气体的质量m = pVM/(RT)
一定质量的气体,由一个状态(参量值为p1、V1、T1)经过任意一个热力学过程(不必是恒值过程)变成另一状态(参量值为p2、V2、T2),根据状态方程,可得到关系式:p1V1/T1= p2V2/T2 (6)
对(5)变换,还可计算单位体积空间内的气体分子数目和气体质量,即气体分子数密度n(m-3)和气体密度p(kg/m3)
n = mNA/MV = pNA/RT= p/kT (7)
p = m/V =pM/RT (8)
系数k = R/NA = 1.38×1023J/K称为波尔兹曼常数。
二、气体分子运动论基础
1. 处于平衡状态的理想气体分子,其热运动速度的分布服从麦克斯韦速度分布定律。气体分子热运动率介于v~v+dv之间的几率为
dN/N = F(v)dv = 4π(mo/2πkT)3/2·exp·(-mov2/2kT)·v2dv (9)
式中F(v)是速率v(m/s)的连续函数,称为速率分布函数。mo = M/NA ,为一个气体分子的质量(kg)。
利用速率分布函数,可以计算出反映分子热运动强度的三种特征速率。最可几速率vm 是在气体分子所具有的各种不同热运动速度中出现几率最大的速度,即与F(v)最大值相对应的v值;所有气体分子热运动速度的算术平均值叫算术平均速度v;把所有气体分子的速度的平方加起来,然后被分子总数除,再开方就得到均方根速度vs。它们的计算公式如下:
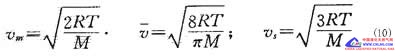
2.理想气体的压力基本公式,将气体分子微观热运动的强弱直接与宏观上的气体压力定量联系起来:
P = 1/3(nmovs2 =1/3(pvs2) (11)
3.气体中一个分子与其它分子每连续二次碰撞之间所走过的路程称为自由程,自由程有长有短,差异很大,但大量自由程的统计平均值却是一定的,称为平均自由程页λ(m)。单一种类气体分子的平均自由程为(12-见下文)
如果是含有k种成份的混合气体,则(13)
式中σ是气体分子的有效直径(m),下标l、j分别代表第1、j种气体成份的参数。
还可定义电子和离子在气体中运动的平均自由程λe和λi(m)。需要强调说明的是,这里所说电子或离子的自由程,是指电子或离子在气体中运动时与气体分子连续二次碰撞间所走过的路程,而没有考虑电子或离子本身之间的碰撞,所以电子和离子平均自由程计算式中出现的都是气体分子的参数,而与电子或离子的空间密度无关。(14)(15)
4.气体分子的某一次自由程取值完全是随机的,但大量自由程的长度分布却服从一定的统计规律。气体分子自由程大于一给定长度χ的几率为(16)
类似地可得出,电子或离子在气体中运动的自由程大于一给定长度χ的几率为(17)(18)
利用这种分布规律,结合平均自由程计算公式(12)~(15),可以计算出做定向运动的粒子束流穿过空间气体时的散失率,或根据所限定的散失率确定空间气体所必须达到的真空度。
例如:一台离子束真空设备中,高能离子流由离子源射向25cm处的靶,若要求离子流与真空室内残余气体分子碰撞的散失率小于5%,那么温度为27oC的残余气体压力应为多少?
根据题意,可知当χ=O.25m时,要求 Pi(λi>χ)≥1%~5%,由(18)式,解出exp(-0.25/λi)≥0.95,则 λi≥0.25/(-ln0.95),即 λi≥4.87m。再将此结果代入(15)式得 kT/πσ2p≥4.87m;取空气的分子有效直径 σ=3.72 × 10-10m,则要求残余气体压力 p≤1.38 × 10-23 × 300/(π×3.722×10-20×4.87),即p≤1.95× 10-3Pa。
5.关于气体分子对所接触固体表面(如容器壁)的碰撞问题,可以从入射方向和入射数量二方面加以讨论。若一立体角dw与面积元ds的法线间的夹角为θ,则单位时间内由dw方向飞来碰撞到ds上的气体分子数目dNθ与cosθ成正比,这就是通常所说的余弦定律:(19)
单位时间内碰撞在固体表面单位面积上的气体分子数目称为气体分子对表面的入射率ν(m-2s-1),其计算式为:(20)
根据平衡状态的假设,气体分子飞离固体表面时的方向分布及数量应与入射相一致,因此仍可按式(19)、(20)计算。克努曾余弦反射定律还说明,不论气体分子的入射方向怎样
其反射都服从(19)式的余弦规律。
6.如果两个相连通的真空容器温度不同,那么内部气体达到状态平衡时的参数也会有差异。在低真空条件下,即粘滞流态时,二容器的平衡条件是压力相等,二容器内气体压力、温度及分子数密度间关系为:
p1 = p2 和 n1/n2 = T2/T1(21)
在高真空条件下,即分子流态时,二容器内气体达到动力平衡的条件是在连通处的入射率γ相等,从而有关系:(22)
这种由于温度不同而引起气体流动,平衡时产生压力梯度的现象,称为热流逸现象。它会给真空测量带来误差。例如某真空电阻炉热场区温度为1800K,通过细管连接的真空规管工作在300K温度下,若规管测得压强为2×10-4Pa,则可由(22)式算得炉内的真实气体压力为(22-1)