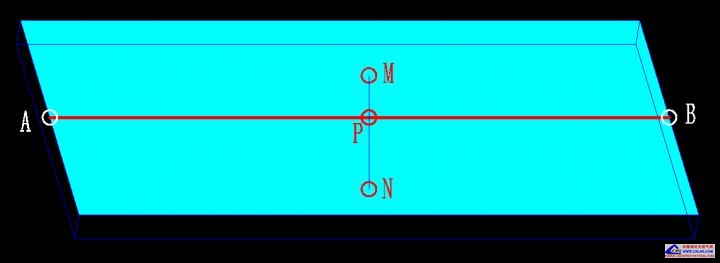
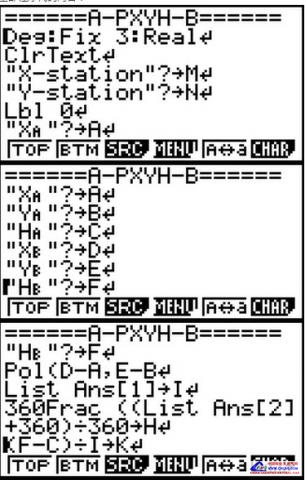
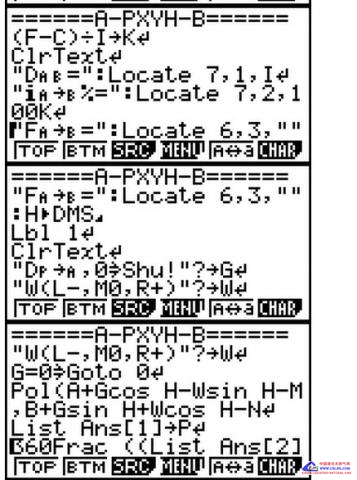
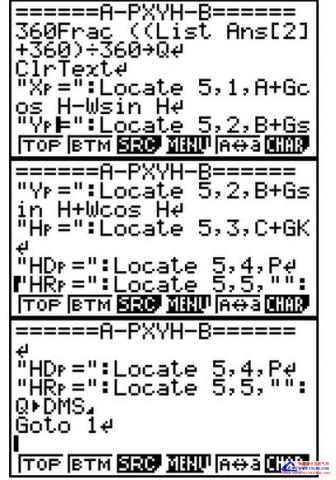
在路桥施工线路中某些桥涵结构物经常遇到如几何模型为四边或者多边形的基坑、砼基础顶面；或者在市政工程城市道路某些管线管槽基坑、基础等管线中轴线（尤其管线位于线路曲线上，两管节之间的管线却是直线的加密点测量计算时）、乃至建筑测量放样施工过程中，往往是已知某构成直线的一条边上的两个点坐标和高程，需要计算加密计算放样出位于该直线段上或者其延长线上多个加密点（甚至包含位于该点垂向的左侧、右侧点位）的坐标和线性纵坡过度后的理论高程。

又由于一般常见此类构筑物体的几何平面顶面高程是保持和中轴线上点高程相等持平的情况，虽然直线中边桩坐标及高程线性过度的计算原理很简单，可在施工现场在某直线段间（及其延长线上）需要加密计算和放样点位很多的情况下，如何快速的得到加密点坐标、如何保持快速计算得到所需点的坐标高程、提高放样效率则尤为十分重要。考虑到编程语句的通用性，不使用复杂的串列矩阵复数等编程语句，采用传统易理解的语法，故在此以9860GII程序代码形式将此正算过程予以发出，可适合于卡西欧9750GII\9860GII\CG20\FD10Pro机型，至于5800计算器可将局部代码语法稍加修改即可使用。几何模型如下图：

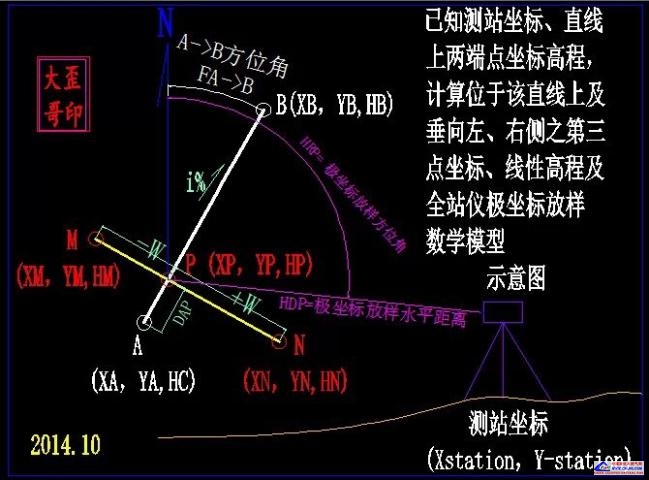
已知对应点A 、P、 B各自左、中、右侧为保持与A B P点高程相等的平面上，某边为直线段上A、B两点（此图以AB为中轴线时为例，当然可以是任意某条边的直线上加密点，只要满足已知求算条件即可）的坐标高程值，求直线上P点坐标以及P点垂向偏距为左侧-W值宽度的M点坐标高程、P点垂向偏距为右侧+W值宽度的N点坐标和高程。（即假定M->P->N横向无横坡，左中右高程相等的计算情况），极坐标放样时则测站坐标也为已知。详细如下图所示。

一、已知和需要输入值为：
以A->B为正方向区分左右。
X-station测站点X坐标值
Y-station测站点Y坐标值
A点坐标高程为（XA,YB,HC)
B点坐标高程为（XB,YB,HB)
A点到P的长度值输入为DAP（程序提示符号是DP->A)，当P点在A->B方向上时输入+值，当在B->A延长线方向上时输入-值。输入0则重新开始另外一段AB直线间输入计算。
MP或者PN值为W，MP时W输入-值，PN时W输入+值，P点时W输入0.（程序提示为W(L-,M0，R+））
三、计算所得：
DA->B= 为A、B两点间的水平距离长度值
i%=为A->B方向的纵向%坡度。
FA->B为A->B方向的方位角
XP ，YP， HP为所求P点或者M 或者N点的坐标和线性高程值。（注：程序此处M P N三点高程是以相等为不考虑横坡是平的情况，如果有横坡，则可计算出P点高程后自己另外根据PM\PN的横坡计算M、N点的高程）
HDP=、HRP=为极坐标放样时测站至当前所计算的P（或者M或者N）点的 放样平距、放样方位角。如果只要坐标高程不用极坐标法放样，则程序开始时测站坐标可输入为（0，0），则可忽略不必理会此项显示。
相关9860GII程序代码逐屏幕显示图片如下（ 程序已经验证，计算无误，可放心使用）：
程序名称：A-PXYH-B
全部程序代码内容：

相关程序g1m格式程序文件包下载链接：
http://pan.baidu.com/s/1nt9M2QP 请复制用电脑下载！
fx-5800计算器需要将Clrtext修改为cls 、将List Ans[1]去除，将
List Ans[2]修改为对应式子后面的H和Q即可；FD10Pro、5800计算器均可去除?后面的->即可。
至于已知A B P三点坐标高程， 对此程序的逆向过程的直线坐标高程反算的过程，因实际使用中并没有此正算放样计算使用频繁，同时因工作忙碌精力有限、暂时使用不多故不再继续编制该功能，有兴趣的可以自己编制实现（提示：反算逆向过程可如此实现的目标过程程序思路：已知A B点坐标高程和P点坐标 计算出P点相对A点的距离 再根据PA和A点高程解算出P点在AB间坡度上所形成的线性理论高程以及P点到AB的垂距用正负号判断出其位于左还是右侧，同样考虑P点与M N点是理论线性高程持平相同的，如此全站仪随便实测AB线上或者其延长线上某点P（当然可能是上图中的M、N点）点的坐标高程，输入坐标后计算 然后将实测高程与此计算所得的高程之差值计算就达到了现实现场实际所需要的程序用途目标结果）。此小程序虽然原理甚为简单，不值一提，在实际施工测量实践中多点加密计算时运用甚为广泛，重在快速计算，编制该程序目的对提高测量外业工作计算时的效率尤其重要，并非展示什么测量编程技术与技巧。只有工地测量实践中用到的人，他才能懂其意义之所在。只重视实践测量运用，不搞大套路测量原理陈谷子烂芝麻之类老套路线路平纵曲线坐标高程这些本已存在于各类书籍中的传统理论计算！

另 附记：曾于2010年10月到达四川高速公路时工地闻听一测量员谈及项目上其前任测量主管在测量横断面时，用一个5800计算器程序输入所需要的点间一定的宽度值，在测站上拨转仪器夹角测距控制棱镜确保走到横断面线上进行路基横断面高程测量的运用，说的好似很厉害很神奇一般，当时不禁笑笑说，没什么了不起的，因心中已经明白其解算操作原理无非就是此程序的具体实践运用之一而已,此处姑且不评论其测量横断面采用此法确保点位严格来到横断面线上之测算法是否愚笨的问题，结合此图具体其操作计算进行分析原理算法也即如下：因为我们知道，无论线路平曲线是直线还是曲线，路基各个桩号的横断面线必定是一条直线！
首先用线路坐标计算程序根据里程桩号偏距先计算出路基中、或者左、右边桩横断面上的两个点坐标值但现场不定桩，只是作为A 、B两点的已知坐标值输入上述程序中，然后在A、B这条横断面直线上按距离A点各个一定的间距DAP值输入求出一系列的P值坐标，同时用程序所显示的测站到所计算的P点方位角、水平距离来控制使得棱镜来到该P点必定在A B间直线段上（或者其延长线上），然后测得其地面高程，作为该桩号横断面测量的各点高程，其各个加密P点距离A点的距离值DAP就是整理后就是对应的横断面偏距值，当然此时他的操作以A点选择为中桩最方便。不足为奇，仅仅举此一例，说明实践中所谓的神奇的测量高手们的运用原理，至于其他更多的巧妙实践运用，自己如果善思多想根据原理自行变通，那么此类小小程序则必将在实际测量外业过程中会有所大用途，某些特殊满足此测量几何模型的情况下所进行的程序计算将会比手工分步骤逐个计算更加便捷高效。