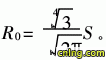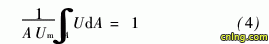多孔泡沫金属换热器内部的非热力学平衡
李菊香1, 涂善东2
(1.南京工业大学能源学院,南京210009; 2.华东理工大学机械与动力工程学院,上海200237)
摘要:应用Brinkman-extended Darcy流动模型,对恒热流密度条件下,方形轴流式多孔泡沫金属换热器内流体与泡沫金属之间的瞬时局部非热力学平衡情况进行了分析。结果表明:当流体在低孔隙率、低ppi数的多孔泡沫金属通道内低速流动,以及当流体和多孔泡沫金属间存在较大的导热能力差异时,两者间的瞬时局部温差较大,不可忽略。
关键词:多孔泡沫金属;管壳式换热器;非热力学平衡
中图分类号:TB383.4; TK124文献标志码:A
关于多孔泡沫金属内流体的流动和传热的研究始于20世纪后半叶[1-3]。目前,国内外对多孔泡沫金属换热器内传热的研究正在由瞬时局部热力学平 衡向着瞬时局部非热力学平衡[4-8]的方向发展。瞬时局部热力学平衡理论认为,局部的流体与多孔泡沫金属之间时刻保持着温度相等的热平衡状态。但事实上,尽管在稳态传热过程中,由于多孔泡沫金属 孔隙参数的影响,流体与多孔泡沫金属之间存在着 热物性尤其是导热能力的差异等,使得流体与多孔泡沫金属之间不可能保持瞬时局部的热平衡状态。到目前为止,有关多孔泡沫金属换热器内流体与多孔泡沫金属之间的瞬时局部温差具体有多大,以及 与哪些因素有关等鲜见报道。本文应用Brinkman- extended Darcy流动模型,对处于恒热流密度条件下,管内、外分别填充多孔泡沫金属的方形轴流式换热器内部流体与多孔泡沫金属之间的瞬时局部非热 力学平衡情况进行了分析。
1 基本假设及数学描述
常压换热器通常为内含多支圆形横截面管和方形管外壳体通道的结构。当传热管为正方形或正三角排列时,常压多孔泡沫金属换热器的结构如图1所示。壳程流体的所有单元流通区域根据传热管的所在位置分为两种:内部管间区域(图1中的位置 1)和区域四周均为绝热边界的全角点管间区域。壳程平直边界上的单元管间区域可认为一部分符合内部管间区域的特征,另一部分符合全角点管间区域 的特征。
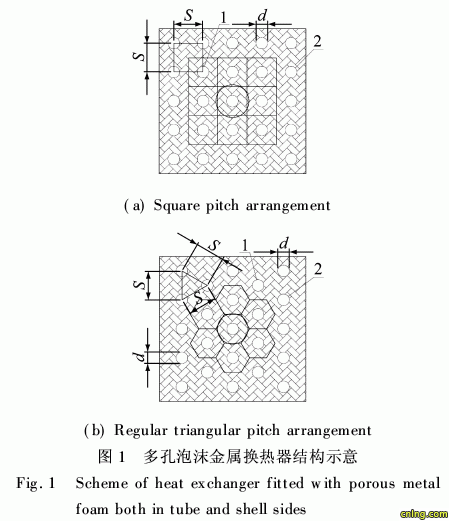
本文基本假设如下:(1)流体流动服从Brink- man-extended Darcy模型;(2)多孔泡沫金属为均匀介质;(3)流体为不可压缩;(4)流体的流动为定常;(5)流体和多孔泡沫金属均为常物性;(6)忽略 热弥散效应;(7)整个管内、外通道内的流动和传热都处于充分发展状态;(8)忽略管壁的导热热阻和管壁与多孔泡沫金属间的接触热阻。无论传热管是正方形排列还是正三角形排列, 换热器内壳程的内部管间区域为一个中心去除管截 面后的正方形或正六边形,均可简化成与其流通面 积相当的圆环区域,如图2所示,传热管正方形排列 时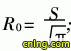 传热管正三角形排列时
传热管正三角形排列时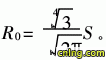
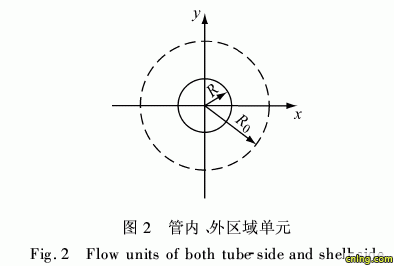
建立圆柱坐标系(r,z),流体的动量方程和流体 与多孔泡沫金属的能量方程分别如下:

本文应用有限差分法以平均温度为50℃的空 气作为单相流体对上述方程组进行了数值计算,由于各方程均为线性,且管、壳程的流动和传热的边界条件都较为简单,因而计算结果只存在迭代过程的累计误差和舍入误差。
2 管内的非热力学平衡
图3为恒热流密度加热条件下平均温度为50 ℃的空气以1 m/s的平均流速在管内流动时截面上无因次过余温度的径向分布,管内填充的多孔泡沫 金属为8 ppi、孔隙率0.95的多孔泡沫铜。图中的横坐标n是以管中心为起点的径向节点数。从图3可知,由于流体处在被加热的条件,除管壁处以外, 多孔泡沫金属的温度高于流体的温度,两者之间存在一个非常明显的无因次过余温差,尤其是在远离管内壁的管中心大部分区域范围内,这说明考虑流体与多孔泡沫金属之间的瞬时局部非热力学平衡非常有必要。
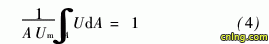





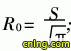 传热管正三角形排列时
传热管正三角形排列时