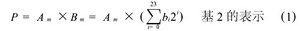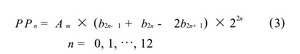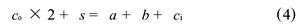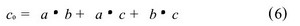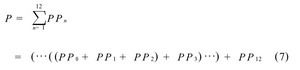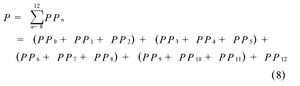免职声明:本网站为公益性网站,部分信息来自网络,如果涉及贵网站的知识产权,请及时反馈,我们承诺第一时间删除!
This website is a public welfare website, part of the information from the Internet, if it involves the intellectual property rights of your website, please timely feedback, we promise to delete the first time.
电话Tel: 19550540085: QQ号: 929496072 or 邮箱Email: Lng@vip.qq.com
摘要:随着计算机和信息技术的快速发展, 人们对微处理器的性能要求越来越高。乘法器完成一次乘法操作的周期基本上决定了微处理器的主频, 因此高性能的乘法器是现代微处理器中的重要部件。本文介绍了32 位浮点阵列乘法器的设计, 采用了改进的Booth 编码, 和Wallace树结构, ..
|
随着计算机和信息技术的快速发展, 人们对微处理器的性能要求越来越高。乘法器完成一次乘法操作的周期基本上决定了微处理器的主频, 因此高性能的乘法器是现代微处理器中的重要部件。本文介绍了32 位浮点阵列乘法器的设计, 采用了改进的Booth 编码, 和Wallace树结构, 在减少部分积的同时, 使系统具有高速度, 低功耗的特点, 并且结构规则, 易于VLSI的实现。
1 乘法计算公式 32 位乘法器的逻辑设计可分为: Booth编码与部分积的产生, 保留进位加法器的逻辑, 乘法阵列的结构。
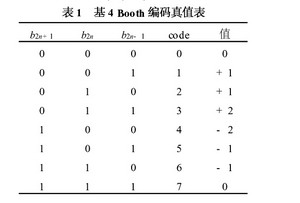
1.1 Booth编码与部分积的逻辑设计 尾数的乘法部分,本文采用的是基4 Booth编码方式, 如表1。首先规定Am和Bm表示数据A和B的实际尾数,P 表示尾数的乘积, PPn表示尾数的部分积。浮点32 位数, 尾数是带隐含位1 的规格化数, 即: Am =1×a22a21….a0和Bm = 1 ×b22b21.…b0, 由于尾数全由原码表示,相当于无符号数相乘, 24 × 24 位尾数乘积P 的公式为:
1.2 乘法器的阵列结构 本文采用的是3-2 加法器, 输入3 个1 位数据: a, b,ci; 输出2 个1 位数据: s, Co。运算式如下:
其逻辑表达式如下:
当每个部分积PPn 产生之后, 将他们相加便得到每个乘法操作的结果。相加的步骤有很多, 可采用的结构和加法器的种类也很多。比如串行累加:
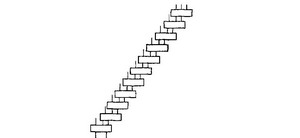
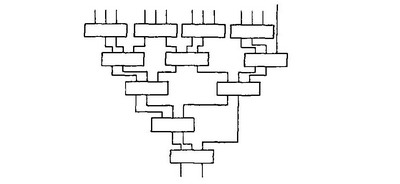
而Wallace 树的乘法阵列如下:
加法器之间的连接关系如图1, 图2 所示, 或者从公式(7) 与(8) 中可以看出, 图1中串行累加的方法延迟为11个3-2 加法器的延迟, 而图2中, Wallace树延迟为5个3 -2加法器的延迟。图1的延迟比图2的延迟大。
图1 串行累加
图2 Wallace 树 2 32 位浮点乘法器的设计 本文是针对IEEE754 单精度浮点数据格式进行的浮点乘法器设计。IEEE754 单精度浮点格为32位, 如图3 所示。设A ,B均为单精度IEEE754格式, 他们的符号位, 有效数的偏移码和尾数部分分别用S , E 和M来表示。双精度和单精度采用的运算规则是一致的, 只是双精度的位长增加了一倍, 双精度是64位, 其中尾数52位, 指数11位, 1位符号位。所以提高了精度范围。
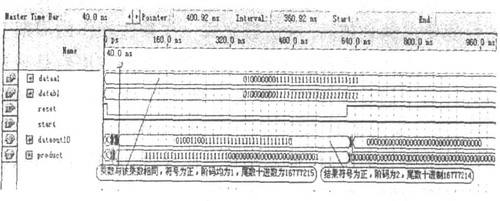
图3 32 位浮点数据格式 32 位浮点数据格式: A = (- 1) S ×M ×2E-127。其中乘法器运算操作分4步进行。 (1) 确定结果的符号, 对A 和B 的符号位做异或操作。 (2) 计算阶码, 两数相乘, 结果的阶码是两数的阶码相加, 由于A 和B 都是偏移码, 因此需要从中减去偏移码值127,得到A 和B 的实际阶码, 然后相加, 得到的是结果的阶码, 再把他加上127, 变成偏移码。 (3) 尾数相乘,A 和B 的实际尾数分别为24位数, 即1×Ma 和1×Mb, 最高位1是隐藏位, 浮点数据格式只显示后23位, 所以尾数相乘结果应为一个48位的数据。 (4) 尾数规格化, 需要把尾数相乘的48位结果数据变成24 位的数据, 分3步进行: ① 如果乘积的整数位为01, 则尾数已经是规格化了;如果乘积的整数位为10, 11, 则需要把尾数右移1位, 同时把结果阶码加1。 ② 对尾数进行舍入操作, 使尾数为24位, 包括整数的隐藏位。 ③ 把结果数据处理为32位符合IEEE浮点数标准的结果。包括1位符号位, 8位结果阶码位, 结果23尾数位。 3 32 位浮点乘法器的实现与仿真 图4 列出本设计的FPGA 仿真结果。图中data1是被乘数, data2是乘数, reset是清零信号, 高有效。start 是开始信号, 也是高有效。dataout10是两个浮点32 位数相乘, 进行规格化以后的结果, 是一个32 位数。Product 是24位尾数相乘的结果, 是一个48位数。
图4 32 位浮点乘法器的仿真结果 整个设计采用了VHDL和Verilog HDL语言进行结构描述, 如果采用的是上华0.5 的标准单元库, 并用Synopsys DC 进行逻辑综合, 其结果是完成一次32位浮点乘法的时间为30ns, 如果采用全定制进行后端版图布局布线, 乘法器性能将更加优越。 4 结 语 本文给出了32 位浮点乘法器的设计, 浮点算法具有高精度性以及较宽的运算范围, 使得乘法的设计更能够满足工程和科学计算的要求, 电路的设计、模拟和实现均采用Altera Quartus II 4.1开发工具。采用的器件EPF10K100EQ 240-1, 逻辑单元是1914个, PIN的数量是147,本设计采用了一系列的算法和结构, 如采用Booth编码的方法和Wallace树的结构, 使得系统具有高速度特点 |