双曲函数

　　在数学中，双曲函数类似于常见的三角函数（也叫圆函数）。基本双曲函数是双曲正弦“sinh”，双曲余弦“cosh”，从它们导出双曲正切“tanh”等。也类似于三角函数的推导。反函数是反双曲正弦“arsinh”（也叫做“arcsinh”或“asinh”）以此类推。
　　因为双曲函数出现于某些重要的线性微分方程的解中，譬如说定义悬链线和拉普拉斯方程。
　　双曲函数接受实数值作为叫做双曲角的自变量。在复分析中，它们简单的是指数函数的有理函数，并因此是完整的。

 

定义

　　双曲函数（Hyperbolic Function）包括下列六种函数：
　　sinh / 双曲正弦： sinh(x) = [e^x - e^(-x)] / 2
　　cosh / 双曲余弦： cosh(x) = [e^x + e^(-x)] / 2
　　tanh / 双曲正切： tanh(x) = sinh(x) / cosh(x)=[e^x - e^(-x)] / [e^x + e^(-x)]
　　coth / 双曲余切： coth(x) = cosh(x) / sinh(x) = [e^x + e^(-x)] / [e^(x) - e^(-x)]
　　sech / 双曲正割： sech(x) = 1 / cosh(x) = 2 / [e^x + e^(-x)]
　　csch / 双曲余割： csch(x) = 1 / sinh(x) = 2 / [e^x - e^(-x)]
　　其中，
　　e是自然对数的底
　　e≈2.71828 18284 59045...= 1/0! + 1/1! + 1/2! + 1/3! + 1/4! + 1/5!...+ 1/n! +...
　　e^x 表示 e的x次幂,展开成无穷幂级数是:
　　e^x=x^0/0! + x^1/1! + x^2/2! + x^3/3! + x^4/4! + x^5/5!...+ x^n/n! +...
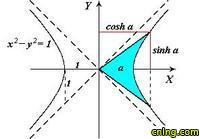
　　如同点 (cost,sint) 定义一个圆，点 (cosh t, sinh t) 定义了右半直角双曲线 x^2 − y^2 = 1。这基于了很容易验证的恒等式
　　cosh^2(t) - sinh^2(t) = 1
　　和性质 t > 0 对于所有的 t。
　　双曲函数是带有复周期 2πi 的周期函数。
　　参数 t 不是圆角而是双曲角，它表示在 x 轴和连接原点和双曲线上的点 (cosh t, sinh t) 的直线之间的面积的两倍。
　　函数 cosh x 是关于 y 轴对称的偶函数。
　　函数 sinh x 是奇函数，就是说 -sinh x = sinh -x 且 sinh 0 = 0。

 

实变双曲函数图像的基本性质

　　y=sinh(x).定义域：R.值域：R.奇函数.函数图像为过原点并且穿越Ⅰ,Ⅲ象限的严格单调递增曲线,当x->+∞时是(1/2)e^x的等价无穷大.函数图像关于原点对称.
　　y=cosh(x).定义域：R.值域：[1,+∞).偶函数.函数图像是悬链线，最低点是(0,1),在Ⅰ象限部分是严格单调递增曲线，当x->+∞时是(1/2)e^x的等价无穷大.函数图像关于y轴对称.
　　y=tanh(x).定义域：R.值域：(-1,1).奇函数.函数图像为过原点并且穿越Ⅰ,Ⅲ象限的严格单调递增曲线.其图像被限制在两渐近线y=1和y=-1之间.lim[x->+∞,tanh(x)=1],lim[x->-∞,tanh(x)=-1].
　　y=coth(x).定义域：{x|x≠0}.值域：{x||x|>1}.奇函数.函数图像分为两支,分别在Ⅰ,Ⅲ象限,函数在(-∞,0)和(0，+∞)分别单调递减.垂直渐近线为y轴，两水平渐近线为y=1和y=-1.lim[x->+∞,coth(x)=1],lim[x->-∞,coth(x)=-1].
　　y=sech(x).定义域：R.值域：(0,1].偶函数.最高点是(0,1),函数在(0,+∞)严格单调递减.x轴是其渐近线.lim[x->∞,sech(x)]=0.
　　y=csch(x).定义域：{x|x≠0}.值域：{x|x≠0}.奇函数.函数图像分为两支,分别在Ⅰ,Ⅲ象限,函数在(-∞,0)和(0，+∞)分别单调递减.垂直渐近线为y轴，两水平渐近线为x轴.lim[x->∞,csch(x)]=0.

 

与三角函数的关系

　　双曲函数与三角函数有如下的关系:
　　* sinh x = -i * sin(i * x)
　　* cosh x = cos(i * x)
　　* tanh x = -i * tan(i * x)
　　* coth x = -i * cot(i * x)
　　* sech x = sec(i * x)
　　* csch x = i * csc(i * x)
　　i 为虚数单位,即 i * i = -1

 

恒等式

　　与双曲函数有关的恒等式如下:
　　cosh^2(x) - sinh^2(x) =1
　　coth^2(x)-csch^2(x)=1
　　tanh^2(x)+sech^2(x)=1
　　* 加法公式：
　　sinh(x+y) = sinh(x) * cosh(y) + cosh(x) * sinh(y)
　　cosh(x+y) = cosh(x) * cosh(y) + sinh(x) * sinh(y)
　　tanh(x+y) = [tanh(x) + tanh(y)] / [1 + tanh(x) * tanh(y)]
　　* 减法公式：
　　sinh(x-y) = sinh(x) * cosh(y) - cosh(x) * sinh(y)
　　cosh(x-y) = cosh(x) * cosh(y) - sinh(x) * sinh(y)
　　tanh(x-y) = [tanh(x) - tanh(y)] / [1 - tanh(x) * tanh(y)]
　　* 二倍角公式：
　　sinh(2x) = 2 * sinh(x) * cosh(x)
　　cosh(2x) = cosh^2(x) + sinh^2(x) = 2 * cosh^2(x) - 1 = 2 * sinh^2(x) + 1
　　* 半角公式：
　　cosh^2(x / 2) = (cosh(x) + 1) / 2
　　sinh^2(x / 2) = (cosh(x) - 1) / 2
　　双曲函数的恒等式都在圆三角函数有相应的公式。Osborn's rule指出：将圆三角函数恒等式中，圆函数转成相应的双曲函数，有两个sinh的积时(包括coth^2(x), tanh^2(x), csch^2(x), sinh(x) * sinh(y))则转换正负号，则可得到相应的双曲函数恒等式。如
　　* 三倍角公式：
　　sin(3 * x) = 3 * sin(x) − 4 * sin(2 * x)
　　sinh(3 * x) = 3 * sinh(x) + 4 * sinh(2 * x)

 

反双曲函数

　　反双曲函数是双曲函数的反函数. 它们的定义为:
　　arsinh(x) = ln[x + sqrt(x^2 + 1)]
　　arcosh(x) = ln[x + sqrt(x^2 - 1)]
　　artanh(x) = ln[sqrt(1 - x^2) / (1 - x)] = ln[(1 + x) / (1 - x)] / 2
　　arcoth(x) = ln[sqrt(x^2 - 1) / (x - 1)] = ln[(x + 1) / (x - 1)] / 2
　　arsech(x) = ± ln[1 + sqrt(1 - x^2) / x]
　　arcsch(x) = ln[1 - sqrt(1 + x^2) / x] , 如果 x < 0
　　ln[1 + sqrt(1 + x^2) / x] , 如果 x > 0
　　其中,
　　sqrt 为 square root 的缩写 , 即平方根

 

双曲函数与反双曲函数的导数

　　(sinh(x))'=cosh(x)
　　(cosh(x))'=sinh(x)
　　(tanh(x))'=sech^2(x)
　　(coth(x))'=-csch^2(x)
　　(sech(x))'=-sech(x)tanh(x)
　　(csch(x))'=-csch(x)coth(x)
　　(arcsinh(x))'=1/sqrt(x^2+1)
　　(arccosh(x))'=1/sqrt(x^2-1) (x>1)
　　(arctanh(x))'=1/(1-x^2) (|x|<1)
　　(arccoth(x))'=1/(1-x^2) (|x|>1)

 

双曲函数与反双曲函数的不定积分

　　∫sinh(x)dx=cosh(x)+c
　　∫cosh(x)dx=sinh(x)+c
　　∫sech^2(x)dx=tanh(x)+c
　　∫csch^2(x)dx=-coth(x)+c
　　∫sech(x)tanh(x)dx=-sech(x)+c
　　∫csch(x)coth(x)dx=-csch(x)+c
　　∫tanh(x)dx=ln(cosh(x))+c
　　∫coth(x)dx=ln|sinh(x)|+c
　　∫sech(x)dx=arctan(sinh(x))+c=2arctan(e^x)+c1=2arctan(tanh(x/2))+c2
　　∫csch(x)dx=ln|coth(x)-csch(x)+c=ln|tanh(x/2)|+c
　　∫[1/sqrt(x^2+1)]dx=arcsinh(x)+c=ln(x+sqrt(x^2+1))+c
　　∫[1/sqrt(x^2-1)]dx=sgn(x)arccosh|x|+c=ln|x+sqrt(x^2-1)|+c
　　(sgn是符号函数.sgn(x)=x/|x|,x≠0;sgn(x)=0,x=0)

 

双曲函数与反双曲函数的级数表示

　　sinh(z)=z+z^3/3!+z^5/5!+z^7/7!+...+z^(2k-1)/(2k-1)!+... (z∈C)
　　cosh(z)=1+z^2/2!+z^4/4!+z^6/6!+...+z^(2k)/(2k)!+... (z∈C)
　　arcsinh(z)=z-(1/6)z^3+(3/40)z^5-(5/112)z^7+...+(-1)^k[(2k-1)!!/(2k)!!][z^(2k+1)/(2k+1)]+... (|z|<1)
　　arctanh(z)=z+z^3/3+z^5/5+z^7/7+...+z^(2k-1)/(2k-1)+... (|z|<1)

 

悬链线(Catenary)

　　形如y=a cosh(x/a)(a为常数)的函数的图象又叫悬链线,可以由柔软的绳子得到,有点象抛物线,但其实两者差距很大.据说莱布尼兹(Leibniz)于1690年最先解出悬链线方程,惠更斯(Huygens)和伯努利兄弟(Jacob Bernoulli,Johann Bernoulli)随其后.惠更斯在1691年把悬链线命名为catenary.
　　悬链线与抛物线有这样的关系:悬链线是直线上滚动的抛物线的焦点的运动轨迹.悬链线的顶点的渐开线是曳物线(tractrix).这条曳物线的渐进线称为悬链线的准线,悬链线绕准线旋转形成的曲面叫做悬链面.